좀더 정확하고, 빠르게 이해해 보자. ^^
4.1 optimization 개요
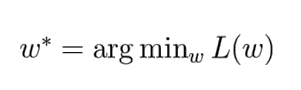
최적화(optimization)란, 바로 저 한 줄이다.
argmin이란 최솟값을 뜻한다 즉, 위의 식은 L(w) (== Loss Function)을 최솟값으로 만들기위한 w를 찾는다는것이다.
즉, 위의 정의는 “최적화란, 손실함수를 최솟값으로 만드는 W를 찾는 것”이다.
3강에서 우리는 손실함수 SVM (힌지로스)과 크로스엔트로피 함수를 배웠습니다. 일반적으로 머신러닝에서 손실함수는 회귀모델에는 평균제곱오차(MSE)를 분류모델에는 크로스 엔트로피(CEE)를 많이 사용합니다.
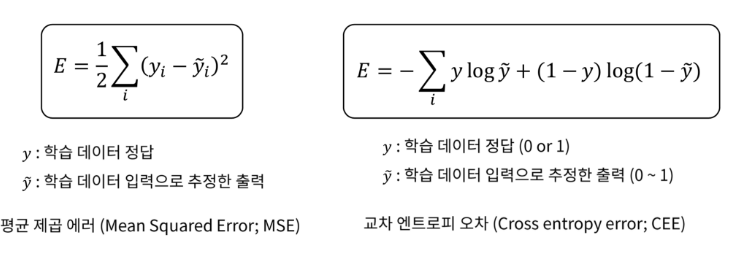
이 손실함수를 최소화 하기 위해서 사용되는 최적화 방법은 경사하강법과 역전파입니다. 강의의 순서상 경사하강법과 뉴럴네트웍, 오차역전법 순으로 블로그가 정리되겠지만, 무엇보다 전체적인 이해가 중요하기 때문에 먼저 아래의 링크를 통해 선행학습이 필요합니다.
CS231n 강의를 듣기전에, CS231n 강의의 3강: 손실함수, 4강:경사하강법, 5강:뉴럴네크워크 6강:오차역전법의 범위를 30분짜리 2Lec으로 구성된 아래의 강의를 먼저 듣고, 간단한 미분 연산으로 머신러닝 최적화 방법중 하나인 경사하강법을 계산해 보는것을 추천합니다.
- 1. 김성범 단장의 뉴럴네트워크 모델1 (구조, 비용함수, 경사하강법)
- 2. 김성범 단장의 뉴럴네트워크 모델2 (오차 역전법)
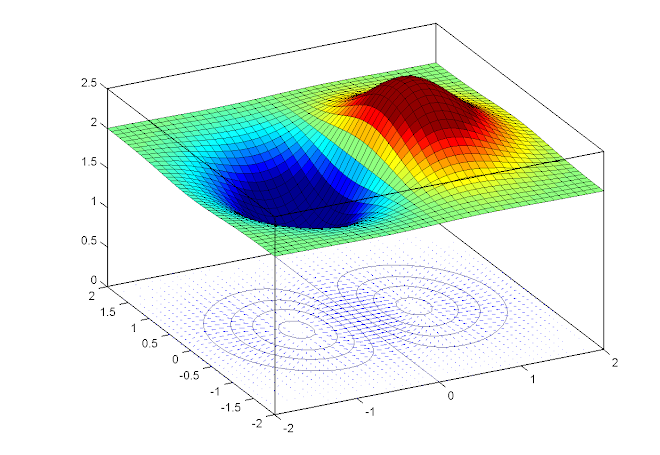
위의 손실함수를 시각화 해보면 아래 그림과 같습니다.
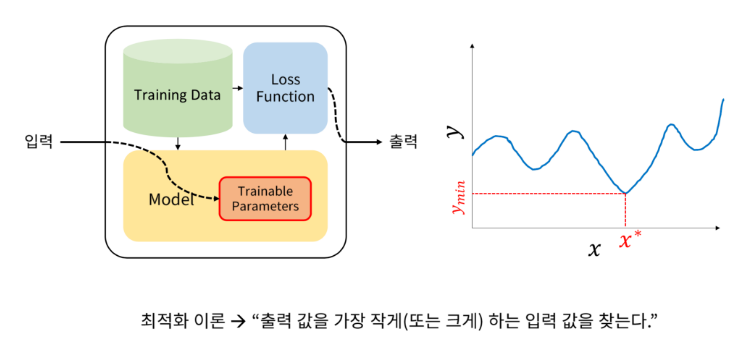
저런 그래프가 나오기 때문에 우리는 경사면을 따라 최솟점으로 내려간다는 표현으로 로스함수 최적화 방법인 경사하강법(gradient decent)를 배울 수 있습니다.

그럼 어디서 부터 기울기를 찾아볼까요? 아니 비용이 작게나오는 W를 어떻게 찾아 낼까요?
강의에서는 Random Search 를 소개합니다. 랜덤하게 선택한 W를 입력하여 학습한 후 낮은 loss가 나올 때까지 계속해서 학습하는 것입니다. 아래 코드는 weight matrix에 해당하는 많은 random value를 만들어내고 각기 다른 matrix별 loss를 구한 후 lowest value를 찾아가는 과정을 반복하는 것입니다. 이전에 찾은 best W matrix와 test data를 내적하여 나온 score 에서 가장 큰 (가장 좋은) 값들을 찾아 평균을 내주는 과정입니다.( 이러한 코드는 성능이 매우 좋지 않습니다.)
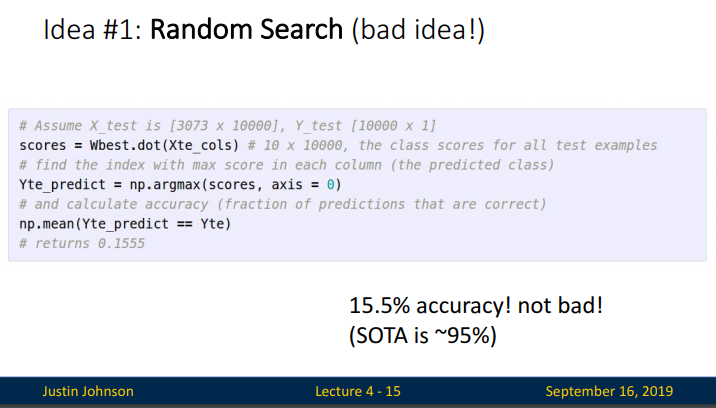
이렇게 찾아진 W로 테스트해본 결과 정확도가 15% 입니다. 무작위로 선택된 W는 가장 단순한 방법으로 가능한 모든 수를 대입해서 찾아보겠는다는 접근인데, 이럴경우 계산의 복잡도가 높아집니다. 시간대비 성능을 올릴 수 있다는 확신도 없습니다. 적게 대입해 보고 Loss를 낮추는 방법이 경사 하강법 (Following the Gradient) 입니다.
두번째로 살펴볼 방법은 Local geomerty한 방법을 생각하는것으로, 어느 한 지점의 기울기를 찾는 방법이 바로 미분 입니다.
미분값을 계산하는 것을 통해서 경사의 방향을 예측할 수 있습니다. 미분이란 어느 지점에서 아주 짧은 순간의 변화값의 비율을 알고 싶을 때 사용하는 수학적 개념으로 경사하강법에서는 비분을 통해 경사면의 방향값을 계산하고, 오차역전법에서는 미분을 통해 현재 출력값에 반영된 가중치(w)가 출력값에서 나온 비용함수에 상대적으로 기여한 양을 계산해서 W를 조정하도록 하는데 이용됩니다.
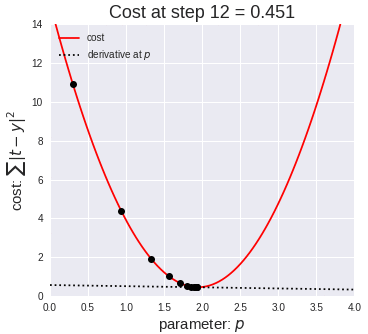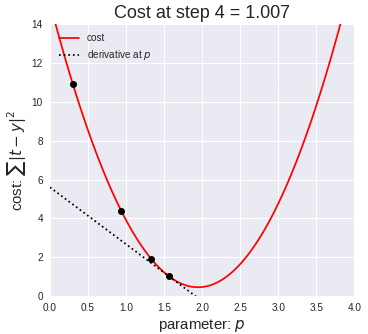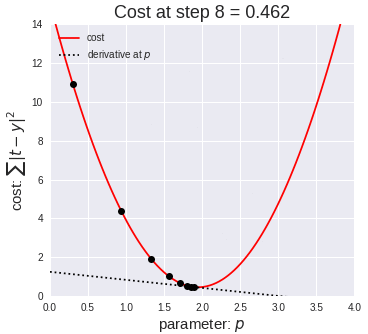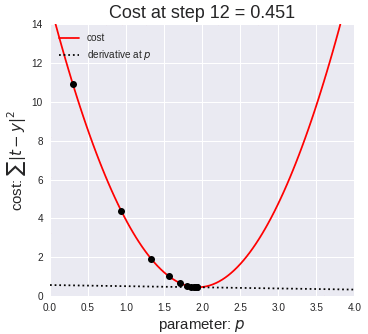
우리는 경사면을 따라 미분을 계산하여 최적점에 도달하는 방법을 이 강의에서 학습할 예정입니다.
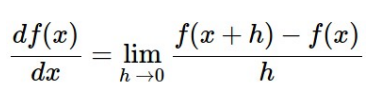
4.2 Computing Gradient
강의에서는 그라디언트를 계산하는 두 가지 방법을 소개합니다. 다른 말로하면, 미분하는 방식에 따라 구 갈래로 나누는 것입니다. 하나는 느리고 근사치를 계산하지만, 쉬운 방법 (수치적 그래디언트:numerical gradient)이고, 다른 하나는 빠르고 정확하지만, 오류가 발생하기 쉬우며 미적분이 필요한 방법(해석적 그래디언트:analytic gradient)입니다.
이 두 방법에 대해서는 수치 그래디언트는 매우 간단한 계산 과정을 보이지만, 계산량이 매우 크며, 근사치(매우 작은 h를 사용한다 하더라도, h가 0의 극한인 경우가 그래디언트의 정의이므로)를 구할 뿐이고, 해석적 그래디언트는 매우 빠르게 계산할 수 있는 그래디언트(근사치 없음)에 대한 직접적인 수식을 유도하지만 수치적 그래디언트와 달리 구현 시 더 오류가 날 수 있습니다. 실제 일반적으로 해석적 그래디언트를 계산한 다음 이를 수치적 그래디언트와 비교하여 구현의 정확성을 확인하는데 이용합니다.
이를 그래디언트 검사(gradient check.)라고 한다는 것까지만 알고 경사하강법과 미니배치 경사하강법, 미니배치 경사하강법의 변형에 대한 부분을 좀 더 자세히 공부해 보겠습니다.

4.3 Gradient Descent
Loss function의 gradient를 계산할 수 있으므로 최적점을 향해 가장 빠르게 내려가는 방법이 Gradient Descent 입니다.

아주 기본적인(== 강의에서는 vanilla라는 표현사용) GD( == Gradient Descent)코드를 통해 살펴보면, 그래디언트는 손실함수에(정규화값이 있을 수 있는) 에타라는 작은값(learning rate)을 곱해서 현 가중치에서 빼주는 방식으로 구하는것을 볼 수 있습니다.
하이퍼 파라미터로 정해진 만큼 반복적으로 이 과정을 수행하게 됩니다.
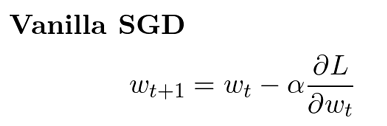
그런데 이 그래디언트 디센트를 바로 적용하기에는 문제점이 있습니다.

그래디언트 디센트 알고리즘에서 그래디언트를 계산하는 부분만 살펴보면 위와 같습니다. 하나의 파라미터 값을 업데이트 하기위해 트레이닝 데이터 셋의 N개를 전부 계산하는 Full-Batch 방식으로 계산되는 것을 알 수 있습니다. 이것은 매우 소모적인 방식입니다. 이 문제를 해결하기 위한 가장 보편적인 방법으로, 트레이닝 데이터셋을 적당히 32개 64개, 128개와 같이 몇 개만 샘플링 Batch에 대하여 계산하는 방식으로 변경하여 적용하는것입니다.
그것이 SGD (Stochastic Gradient Descent):확률적 경사하강법 입니다.
모집단의 로스평균값과 샘플링 batch의 로스 평균값이 크게 다르지 않을것이라고 보는 것입니다. 샘플링값으로 근사하겠다는 의미이고, ‘미니 배치의 그래디언트는 전체 그래디언트에 대한 근사 값을 가질 것이다’라고 보는 것입니다.
그렇다면 SGD로 어떻게 그것이 가능한지 확인해 보겠습니다.

SGD를 적용함으로 계산의 복잡도를 줄일 수 있지만, 몇 가지 문제점이 생깁니다.
문제점을 들어가기 앞서 그래디언트 디센트를 설명하기위한 이미지를 하나 이해하고 넘어가겠습니다.
경사하강법에는 몇가지 문제점이 있습니다. SGD와 같은 업그레이드된 최적화 방법을 적용한다고 해도 경사하강법이 갖는 근본적인 문제입니다
첫째, 노이즈 문제 입니다. Oscillation(진동) 문제라고 하기도 합니다. 바로 적당한 값의 learning rate를 선택하는 것이 너무 어렵다.는 것입니다. 학습률(learning rate)이 낮으면 천천히 가는 대신 최솟값 근처에서 안정적으로 수렴할 수 있지만, 학습률이 높으면 빠르게 가는 대신 최솟값 근처에서 왔다 갔다 주변을 왔다갔다 거리거나 발산해버립니다.이렇게 왔다 갔다 하면서 최솟값을 찾는데 시간을 낭비하는 현상을 Oscillation 문제라고 합니다.
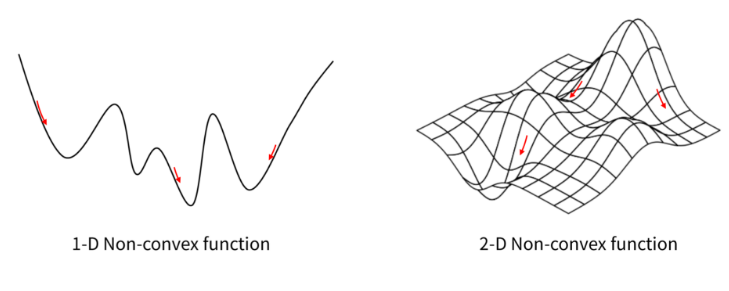
둘째, 극소(Local Minimum) 문제 입니다. 우리는 loss function에서 global minimum 부분 즉, loss가 최소화되는 부분을 찾길 원합니다. 하지만 optimizer가 착각하여 loss function의 수많은 local minimum 중 global minimum에 해당하지 않는 local minimum에 멈추거나 완만한 경사지역 Saddle point 에 빠질 수 있습니다. 우리가 마주칠 대부분의 문제는 Non-convex 함수이므로 단순한 경사하강법으로는 한계가 있습니다.
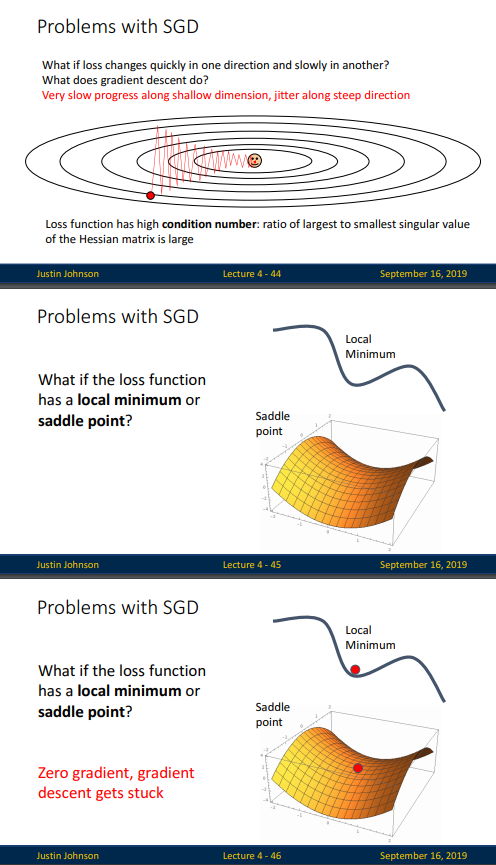
위의 문제가 일반적인 GD의 문제 였다면, SGD의 문제점은 노이즈가 심하다는 것입니다.
경사면을 따라 최적점을 찾아 가기는 하지만, 미니배치를 이용하기 때문에 완만하게 내려가지 못한다는 것입니다.
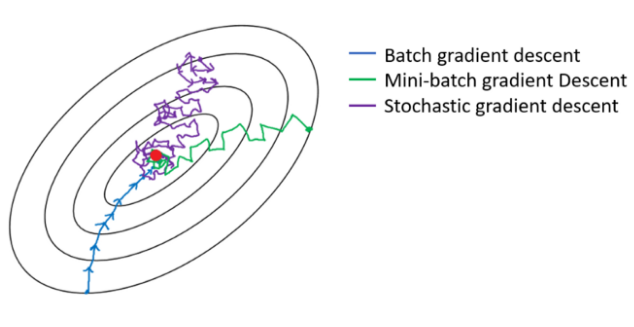
그래서 이러한 문제점들을 보완하기위한 SGD변형 알고리즘에 대해 알아보겠습니다.
4.4 Variants of SGD
(1. monentum / 2.Nestrov Monentum / 3.AdaGrid / 4. RMSprop / 5. Adam)

1.SGD with Momentum (Momentum SGD) : 속도를 빠르게!!
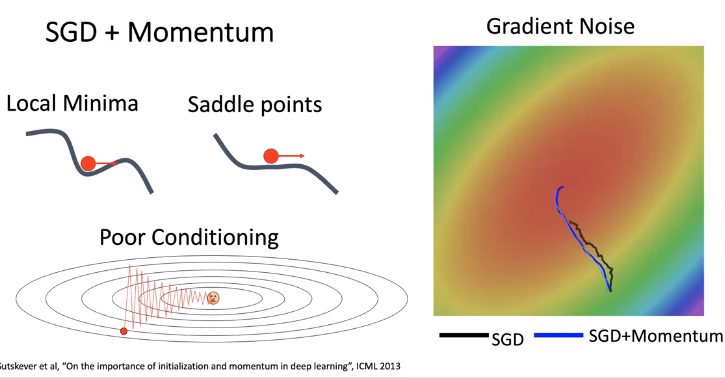
가속도(탄력)의 개념을 추가하여 속도에 gradient를 더한 값으로 gradient descent를 수행하는 방식입니다. SGD가 손실함수를 편미분(접선의 기울기)을 가지고 W를 업데이트 했다면, 모멘텀은 현재의 기울기+이전의 기울기를 포함하여 누적된 가속도로 W를 업데이트 합니다.(물리적 관성의 개념)
- SGD의 문제점들(poor conditioning, local minima/saddle point, gradient noise)을 해결하는데 도움이 됩니다. (velocity를 구할 때, 평균을 구하는 것처럼 noise를 경감시키는 효과가 있다)
- 일반적으로 friction rate ρ를 0.9 혹은 0.99로 사용하고, velocity v의 초깃값으로 0를 사용합니다.
- 단점은 속도는 빠르지만, 과거값을 누적하는 방식이므로 메모리가 더 필요하다. 또한 최적점(global optima)에서도 이전 가속도가 더해지기 때문에 지나치는 현상이 발생합니다.
2.SGD with Nesterov Momentum
SGD모멘텀의 변형방식입니다. 최적점을 지나치는 현상을 개선하기 위해 이전 가속도를 조금 줄여서 반영하는 방식으로 수정된 알고리즘 입니다. 현재 위치에서 gradient를 계산하는 momentum update와는 달리, velocity만으로 update한 지점에서 계산한 gradient를 사용하여 gradient descent를 수행한다.

모멘텀이 현재의 기울기+이전의 기울기로 구하는 방식이었다면, 네스트로브는 현재의 기울기+이전의 기울기를 구한다음 이전 기울기의 누적치를 빼줌으로써 모멘텀의 추월 현상을 줄여준다는 이론이다. (다른말로, 모멘텀을 진행한 상태에서 그 상태에서 기울기를 계산하여 더하는 것이라고 말하기도 함) 하지만 성능상 크게 향상되지 않아서 디표트 = 모멘텀!!
3.AdaGrad (Adepted 1번째 방식)
속도를 높이는 것보다 일직선으로 향하게 하는 방식이다. 모멘텀 방식이 지그재그 현상을 개선하지 못했다면 AdaGrad방식은 w의 업데이트량을 보정함으로써 해결하는 방식이다. 어댑티브 방식을 사용할 경우 아래 그림과 같이 모멘텀 옵티마이져에서 휘어지는 부분을 보다 일직선으로 만들 수 있다.
경사가 완만해지는 구간에서 (skewed space) 느려지는 단점이 있다. 이유는 제곱된 부분이 끊임없이 누적되기 때문에 나누어주는 수가 커져서 W업데이트가 느려지고 결국 0이 된다.
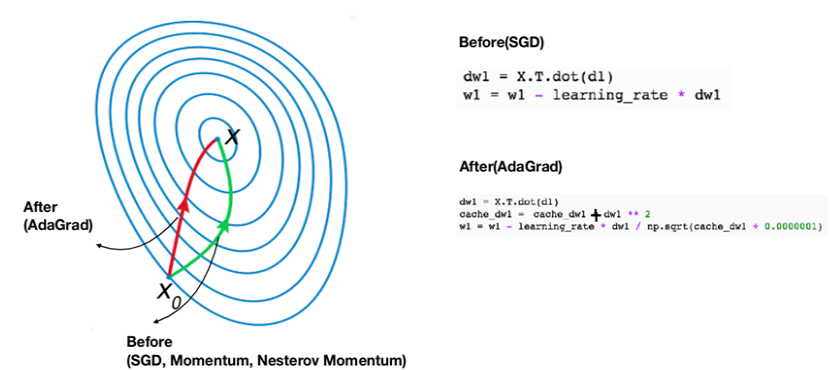
계산 방식은 현재의 기울기(w1)을 그냥 대입는 것이 아니라 제곱하고(음수도 양수가 되도록) 루트씌워서 (크기만 원상복귀하여 마이너스만 제거) 양수로 만든다음 나누어 준다.( +제곱해 준 부분만 누적되어 저장된다.)
지금은 많이 사용하지 않지만, 연구는 활발하게 진행되는 알고리즘 이라고 한다.
4. RMS Prop (Adepted 2번째 방식)
AdaGrad의 제곱부분을 계속해서 누적할 때, 누적값이 너무 커져서 느려지는 부분을 개선한 방식으로, 이전에 제곱되어 누적된 값과 새롭게 제곱되어 누적되는 부분의 반영비율을 decay라는 상수로 조절해주는 방식이다.
예를들어, 만약 decay가 0.9라면 이전의 누적된 기울기(그래디언트)의 제곱은 90%만 반영해서 누적, 현재 그래디언트의 제곱은 10%만 반영하겠다는 것이다.
이럴경우 속도가 느려졌다면, decay를 줄여서 누적값의 반영을 줄인다면, 나누는(분모)부분이 작아져서 업데이트 속도가 올라갈것이라는 알고리즘이다.
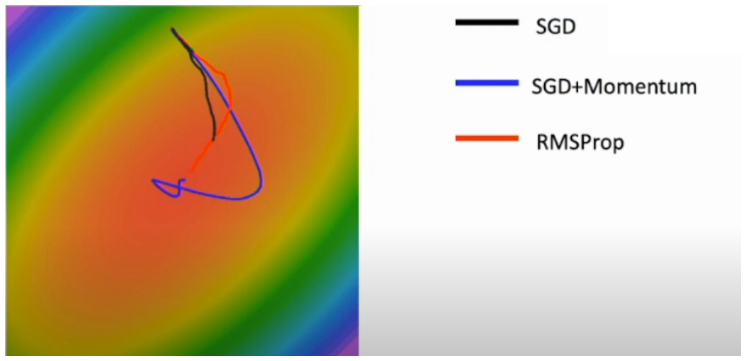
위의 AdaGrad와 마찬가지로 모멘텀의 지그재그 현상은 많이 개선된 듯한 모습니다. 마지막으로 가장 많이 쓰이는 Momentum+RMSProp 을 합친 Adam 알고리즘에 대해 알아보겠습니다.
5.Adam
Adam 은 RMSProp 와 Momentum을 합친 개념입니다. (모멘텀 방식+어댑티브 방식)

Adam의 수식에 대한 자세한 풀이가 알고싶은 분은 링크를 참조하길 바란다. 난 봐도 잘 모르겠는걸… [링크]
Adam은 빠르고 완만하게 잘 가도록 두 알고리즘의 장점만 모아 두었지만, t가 0일때 (시작지점에서) friction coeffitient인 beta2가 0.999가량의 매우 큰 값을 갖게 된다. 이것은 우리가 moment2를 0로 initialize 하였는데 first gradient step에서 moment2는 0에 매우 근접한 값을 갖게되어 moment2를 square root 취하었을때 0에 근접한 값을 갖게하여 결국 시작 step에서 매우큰 gradient step을 갖게된다 이것은 때때로 매우 나쁜 결과로 이끌 수 있다.
- [Adam 논문 링크] 혹시라도 나중에 볼 일이 있을까 싶어서 keep.!!
이런 문제를 극복하기 위해서 위의 코드에 bias correction을 추가시켜준다고 한다.

강의에서는 다음과 같은 하이퍼파라미터를 사용하는것이 좋다고 말한다. 이런건 그냥 묻지않고 쓰는걸로~

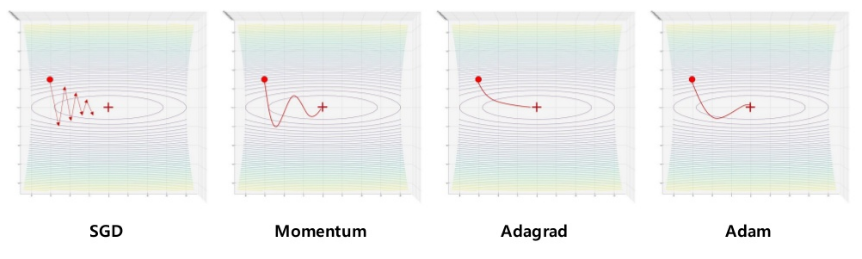
출처 : https://sunnyyanolza.tistory.com/23

